=amstex
=10 R L^1() L^&infin#infty;() 0() 0 ·
BRADLEY J. LUCIER![[*]](/file/16861/Sprite 1984 - 1993.iso/lib/tex/inputs/amstexsiam-sample.tex/footnote.png) "
" "Department of Mathematics, Purdue University,
West Lafayette, Indiana 47907.
The work of the first author was not supported by the
Wolf Foundation.
and
DOUGLAS N. ARNOLD
"Department of Mathematics, Purdue University,
West Lafayette, Indiana 47907.
The work of the first author was not supported by the
Wolf Foundation.
and
DOUGLAS N. ARNOLD![[*]](/file/16861/Sprite 1984 - 1993.iso/lib/tex/inputs/amstexsiam-sample.tex/footnote.png) "
" "Department of Mathematics, University
of Maryland, College Park, Maryland 20742.
"Department of Mathematics, University
of Maryland, College Park, Maryland 20742.
Abstract:
This sample paper illustrates many of the amstex
macros as used with the AmS-TeX SIAM style file.
The AmS-TeX SIAM style file (amstexsiam.sty), which is a modification of
the amsppt style of Michael Spivak, gives authors easy
access to most of the typographical constructions used in SIAM journals.
It does not address the issues of the table of contents
or tables, which must be set using more primitive TEX macros.
1. Introduction
We are concerned with numerical approximations to the so-called
porous-medium equation [#!6!#],
We assume that the initial data u0(x) has bounded support, that
0≤u0≤M, and that
φ(u0)x∈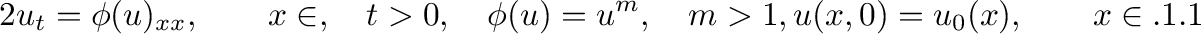 .
It is well known that a unique solution u(x, t) of (1.1) exists,
and that u satisfies
.
It is well known that a unique solution u(x, t) of (1.1) exists,
and that u satisfies
0≤
u≤
M and
 φ
φ(
u( ⋅ ,
t))
x≤
 φ
φ(
u0)
x.

1.2
 , then
(u( ⋅ , t)m-1)x∈
, then
(u( ⋅ , t)m-1)x∈ (see [3]). (This will follow from results presented here, also.)
We also use the fact that the solution u is Hölder continuous in t.
(see [3]). (This will follow from results presented here, also.)
We also use the fact that the solution u is Hölder continuous in t.
2.  error bounds
After a simple definition, we state a theorem
that expresses the error of approximations uh in
terms of the weak truncation error E.
Definition 2.1A definition
is the same as a theorem set in roman
type.
Theorem 2.1
Let {uh} be a family of approximate solutions satisfying
the following conditions for
0≤t≤T:
For all x∈
error bounds
After a simple definition, we state a theorem
that expresses the error of approximations uh in
terms of the weak truncation error E.
Definition 2.1A definition
is the same as a theorem set in roman
type.
Theorem 2.1
Let {uh} be a family of approximate solutions satisfying
the following conditions for
0≤t≤T:
For all x∈ and positive t,
0≤uh(x, t)≤M;
Both u and uh are Hölder–α in x
for some
α∈(0, 1∧1/(m - 1)); uh is right continuous in t;
and uh is Hölder continuous in t on
strips
and positive t,
0≤uh(x, t)≤M;
Both u and uh are Hölder–α in x
for some
α∈(0, 1∧1/(m - 1)); uh is right continuous in t;
and uh is Hölder continuous in t on
strips
 ×(tn, tn+1), with the set {tn} having no
limit points; and
There exists a positive function
ω(h, ε) such that:
whenever
{wε}0 < ε≤ε0 is a family of functions
in
×(tn, tn+1), with the set {tn} having no
limit points; and
There exists a positive function
ω(h, ε) such that:
whenever
{wε}0 < ε≤ε0 is a family of functions
in  X for which
"(a)" there is a sequence of positive numbers ε tending
to zero, such that for these values of
ε,
| wε|∞≤1/ε,
"(b)" for all positive
ε,
| wxε(
X for which
"(a)" there is a sequence of positive numbers ε tending
to zero, such that for these values of
ε,
| wε|∞≤1/ε,
"(b)" for all positive
ε,
| wxε( , t)|
, t)| ≤1/ε2, and
"(c)" for all
ε > 0,
≤1/ε2, and
"(c)" for all
ε > 0,
where p is some number not exceeding 1,
then
| E(uh, wε, T)|≤ω(h, ε).
Then, there is a constant
C = C(m, M, T) such that
|
u -
uh|
∞, ×[0, T]
×[0, T]≤
C
sup


(
u0(
x) -
uh(
x, 0))
w(
x, 0) d
x
+
ω(
h,
ε) +
εα![$\displaystyle \left.\vphantom{
\sup \left \vert\int_\BbbR(u_0(x)-u^h(x,0)) w(x,0) \,dx\right\vert+
\omega(h,\epsilon)+\epsilon^\alpha}\right]$](/file/16861/Sprite 1984 - 1993.iso/lib/tex/inputs/amstexsiam-sample.tex/img20.png)
,

2.1
 X.
ProofLet z be in
X.
ProofLet z be in  X. Because
E(u,
X. Because
E(u, ,
, )≡ 0,
Equation (1.5) implies that
)≡ 0,
Equation (1.5) implies that
 Δuz
Δuz|
T0dx =

 Δu
Δu(
zt +
φ[
u,
uh]
zxx) d
x d
t -
E(
uh,
z,
t),

2.2
where
Δu = u - uh and
φ[
u,
uh] =

.
Extend
φ[u, uh](⋅, t) = φ[u, uh](⋅, 0) for negative t, and
φ[u, uh](⋅, t) = φ[u, uh](⋅, T)
for t > T.![[*]](/file/16861/Sprite 1984 - 1993.iso/lib/tex/inputs/amstexsiam-sample.tex/footnote.png) Fix a point x0 and a number
ε > 0. Let
jε
be a smooth function of x with integral 1 and support in
[- ε, ε],
and let Jδ be a smooth function of
x and t with integral 1 and support in
[- δ, δ]×[- δ, δ]; δ and ε are
positive numbers to be specified later.
We choose
z = zεδ to satisfy
Fix a point x0 and a number
ε > 0. Let
jε
be a smooth function of x with integral 1 and support in
[- ε, ε],
and let Jδ be a smooth function of
x and t with integral 1 and support in
[- δ, δ]×[- δ, δ]; δ and ε are
positive numbers to be specified later.
We choose
z = zεδ to satisfy
The conclusion of the theorem now follows from (2.1) and the fact that
| jε*Δu(x0, t) - Δu(x0, t)|≤Cεα,
which follows from Assumption 2.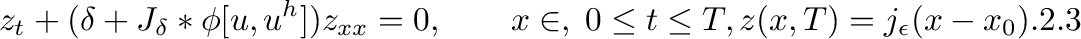 #_no#> 1
L. A. Caffarelli and A. Friedman
Regularity of the free boundary of a gas flow in an
n-dimensional porous medium
Indiana Math. J.
29
1980
361–391
#_no#> 2
K. Hollig and M. Pilant
Regularity of the free boundary for the porous medium equation
MRC Tech. Rep. 2742
#_no#> 3
J. Jerome
Approximation of Nonlinear Evolution Systems
Academic Press
New York
1983
#_no#> 4
R. J. LeVeque
Convergence of a large time step generalization of Godunov's method
for conservation laws
Comm. Pure Appl. Math.
37
1984
463–478
#_no#> 5
A large time step generalization of Godunov's method for systems
of conservation laws
#_no#> 6
B. J. Lucier
On nonlocal monotone difference methods for scalar conservation laws
Math. Comp.
47
1986
19–36
;''ARRAY(0x2ba7150)
#_no#> 1
L. A. Caffarelli and A. Friedman
Regularity of the free boundary of a gas flow in an
n-dimensional porous medium
Indiana Math. J.
29
1980
361–391
#_no#> 2
K. Hollig and M. Pilant
Regularity of the free boundary for the porous medium equation
MRC Tech. Rep. 2742
#_no#> 3
J. Jerome
Approximation of Nonlinear Evolution Systems
Academic Press
New York
1983
#_no#> 4
R. J. LeVeque
Convergence of a large time step generalization of Godunov's method
for conservation laws
Comm. Pure Appl. Math.
37
1984
463–478
#_no#> 5
A large time step generalization of Godunov's method for systems
of conservation laws
#_no#> 6
B. J. Lucier
On nonlocal monotone difference methods for scalar conservation laws
Math. Comp.
47
1986
19–36
;''ARRAY(0x2ba7150)
 "Department of Mathematics, Purdue University,
West Lafayette, Indiana 47907.
The work of the first author was not supported by the
Wolf Foundation.
and
DOUGLAS N. ARNOLD
"Department of Mathematics, Purdue University,
West Lafayette, Indiana 47907.
The work of the first author was not supported by the
Wolf Foundation.
and
DOUGLAS N. ARNOLD φ(u( ⋅ , t))x≤
φ(u( ⋅ , t))x≤ φ(u0)x.
φ(u0)x. 1.2
1.2
 , then
(u( ⋅ , t)m-1)x∈
, then
(u( ⋅ , t)m-1)x∈ (see [3]). (This will follow from results presented here, also.)
We also use the fact that the solution u is Hölder continuous in t.
(see [3]). (This will follow from results presented here, also.)
We also use the fact that the solution u is Hölder continuous in t.
 error bounds
After a simple definition, we state a theorem
that expresses the error of approximations uh in
terms of the weak truncation error E.
Definition 2.1A definition
is the same as a theorem set in roman
type.
Theorem 2.1
Let {uh} be a family of approximate solutions satisfying
the following conditions for
0≤t≤T:
For all x∈
error bounds
After a simple definition, we state a theorem
that expresses the error of approximations uh in
terms of the weak truncation error E.
Definition 2.1A definition
is the same as a theorem set in roman
type.
Theorem 2.1
Let {uh} be a family of approximate solutions satisfying
the following conditions for
0≤t≤T:
For all x∈ and positive t,
0≤uh(x, t)≤M;
Both u and uh are Hölder–α in x
for some
α∈(0, 1∧1/(m - 1)); uh is right continuous in t;
and uh is Hölder continuous in t on
strips
and positive t,
0≤uh(x, t)≤M;
Both u and uh are Hölder–α in x
for some
α∈(0, 1∧1/(m - 1)); uh is right continuous in t;
and uh is Hölder continuous in t on
strips
 ×(tn, tn+1), with the set {tn} having no
limit points; and
There exists a positive function
ω(h, ε) such that:
whenever
{wε}0 < ε≤ε0 is a family of functions
in
×(tn, tn+1), with the set {tn} having no
limit points; and
There exists a positive function
ω(h, ε) such that:
whenever
{wε}0 < ε≤ε0 is a family of functions
in  X for which
"(a)" there is a sequence of positive numbers ε tending
to zero, such that for these values of
ε,
| wε|∞≤1/ε,
"(b)" for all positive
ε,
| wxε(
X for which
"(a)" there is a sequence of positive numbers ε tending
to zero, such that for these values of
ε,
| wε|∞≤1/ε,
"(b)" for all positive
ε,
| wxε( , t)|
, t)| ≤1/ε2, and
"(c)" for all
ε > 0,
≤1/ε2, and
"(c)" for all
ε > 0,
 x∈
x∈

 ≤1/ε2,
≤1/ε2,
 sup
sup 2.1
2.1
 X.
ProofLet z be in
X.
ProofLet z be in  X. Because
E(u,
X. Because
E(u, ,
, )≡ 0,
Equation (1.5) implies that
)≡ 0,
Equation (1.5) implies that
 2.2
2.2